Question Answers
Kinematics
1. Give two examples of the motion in which acceleration is non-zero but velocity is zero?
At the extreme position of the simple harmonic motion, the velocity is zero but the acceleration is non-zero directed towards the extreme position. Similarly, when a body is thrown upward, at the highest point the velocity is zero, but there is acceleration due to gravity acting downwards. These are the two examples in which acceleration is non-zero but velocity is zero.
2. Can an object have an eastward velocity experiencing a westward acceleration? Give reasons.
Yes, an object having eastward velocity can experience a westward acceleration when motion of the object is retarding. In case of retarding motion, the direction of retardation (-a) is opposite to the direction of velocity of the body.
3. Can a body be regarded in a state of rest as well as in motion at the same time? Give an example.
Yes, a body can be regarded in a state of rest with respect to one reference as well as in a state of motion with respect to another reference at the same time. For example, a person sitting in a moving car is in the state of rest with respect to car but in the state of motion with respect to ground.
4. A projectile fixed at an angle 18 ° has certain horizontal range. State another angle of projection for the same horizontal range.
Let R be the horizontal range and θ be the angle of projection. Then we have, $$ R = \frac{u^2 sin 2 \theta}{g} ..... (i)$$
Now, $$sin 2 \theta = sin (180^o - 2 \theta)$$
$$= sin 2 (90^o - \theta)$$ Therefore eqn (i) becomes $$ R = \frac{u^2 sin 2 (90^o - \theta)}{g}..... (ii)$$ This gives the same horizontal range for (90° – θ) being the angle of projection.
Hence, the horizontal range of the projectile fixed at an angle of 180 will have same horizontal range at the angle of (90° – 18°) = 72°.
5. Raindrops hitting the side windows of a car in motion often leave diagonal streaks, why?
When raindrops with velocity Vr hits the side window of a car moving with velocity Vc , the relative velocity Vrc of the raindrop with respect to the car makes an angle θ with vertical as shown in figure.
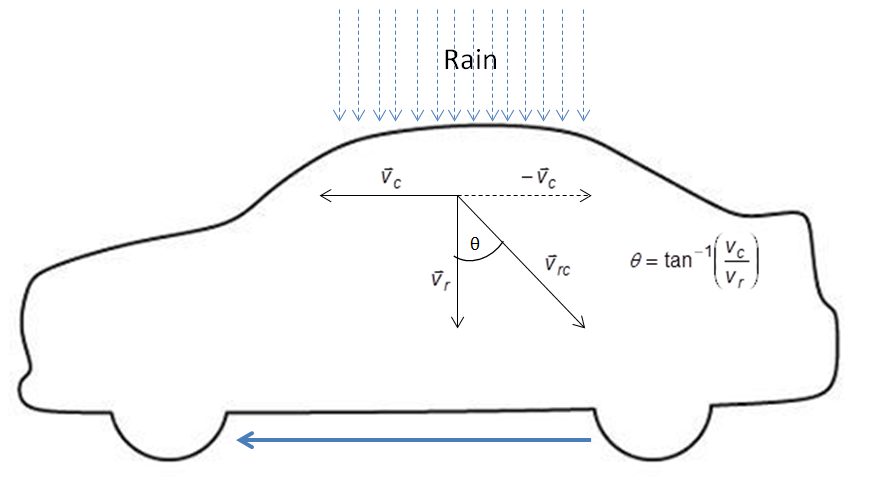
Due to this, raindrops hitting the side windows of a car in motion often leave diagonal streaks.
6. What would be the effect on maximum range in doubling the initial velocity of the projectile?
When a ball is dropped gently from the top of the tower and another ball is thrown horizontally at the same time, the initial vertical velocity for both the balls is zero and their acceleration are equal to g.
We Know, $$ h = ut + \frac{1}{2} gt^2$$ $$h=0 + \frac{1}{2}gt^2 $$ $$ t = \sqrt{\frac{2h}{g}}$$
This is the time required to reach the ground. Since, the height for both the ball is same, the time required for the balls to reach the ground will be same. Hence, both balls hit the ground at the same time.
7. A ball is dropped gently from the top of the tower and another ball is thrown horizontally at the same time, which ball hit the ground earlier? Explain.
The range of the projectile with initial velocity is $$ R = \frac{u^2 sin 2 \theta}{g} ..... (i)$$
If u' be the double velocity, i. e, u' = 2u. Then the range will be given by, $$ R' = \frac{u'^2 sin 2 \theta}{g} = \frac{(2u)^2 sin 2 \theta}{g} = \frac{4u^2 sin 2 \theta}{g} = 4R $$
Hence the maximum range is 4 times as the initial velocity is doubled.
8. Can an object with constant acceleration reverse its direction?
Yes, when the object is thrown upward vertically, the acceleration is equal to acceleration due to gravity = 9.8 ms-2 i. e, acceleration is constant and directed towards the earth. After, attending maximum height the object reverses its direction and falls downward having same acceleration. Hence, an object with constant acceleration can reverse its direction.
9. Can the direction of velocity of a body be changed when its acceleration is constant?
Yes, when body is thrown vertically upward the direction of velocity is in upward direction. After attending maximum height the body falls downward and the direction of velocity changes to downward. But during this motion the acceleration is constant equal to acceleration due to gravity and is always directed downward.
10. A projectile moves in a parabolic path without air resistance. Is there any point at which its acceleration is perpendicular to the velocity?
Yes, the acceleration is perpendicular to the velocity at the highest point of the parabolic path. It is because the vertical component of the velocity is zero and there is only the horizontal component giving horizontal direction of the velocity. And the acceleration due to gravity is directed vertically downwards. So, acceleration is perpendicular to the velocity.
11. A bomb is to be dropped from a moving helicopter on a target on the ground. Explain how it can hit the target.
The bomb should be dropped when the plane is still some distance away from the target on the ground. It is because when the bomb is dropped from the plane along with vertical downward motion it also has horizontal motion with velocity equal to the velocity of plane due to inertia of motion.
12. From a flying aeroplane a body should be dropped in advance to hit the target, why?
The body should be dropped when the plane is still some distance away from the target on the ground. It is because when the bomb is dropped from the plane along with vertical downward motion it also has horizontal motion with velocity equal to the velocity of plane due to inertia of motion.