Question Answers
Viscosity
1. When a smooth flowing stream of water comes out of a faucet, it narrows as it falls. Explain
From the equation of continuity, A1v1 = A1v1
When the stream of water falls, the velocity of the fluid goes on increasing due to action of force of gravity or acceleration due to gravity. As a result, the cross-section area of the fluid decreases as given by above equation. So, the stream of water narrow as it falls.
2. Explain the dimension of the velocity gradient from the definition of the coefficient of viscosity.
According to the definition of the coefficient of viscosity, we get, the expression of velocity gradient as $$\frac{dV}{dx} = - \frac{F}{A\eta}$$
We have
Dimensional formula of $$F = [MLT^{-2}]$$, $$A = [L^2]$$ and $$\eta = [ML^{-1}T^{-1}]$$
Therefore, Dimensional formula of $$\frac{dV}{dx} = \frac{[MLT^{-2}]}{[L^2][ML^{-1}T^{-1}]} = [T^{-1}]$$
3. Why does a flag flatter on strong winds?
During strong winds, the velocity of winds around the flag varies. As a result, the pressure around the flag varies as given by Bernoulli’s equation. $$E=\frac{P}{\rho} + gh + \frac{v^2}{2} = Constant$$ Thus, there is pressure difference with movement of air. Hence, the flags shifts continuously towards the portion of lower pressure and the flag flatters.
4. Explain why a suction effect is experienced by a person standing close to the platform at a station when a fast train passes.
At the region near the fast moving train the velocity of air is high and thus the pressure is low as given by Bernoulli’s principle. The fast moving air between the person and the train, therefore produces a decrease in pressure and the excess of air pressure on the other side. This pushes the person towards the train. Hence, the person standing close to the fast moving train experiences a suction effect.
5. Why are light roofs blown off during cyclones or string winds storms?
During cyclones or strong winds storms, the speed of air above the roof is more whereas those below is very less. Due to high speed of air above the roof, the pressure there will be less as given by Bernoulli's equation, $$E=\frac{P}{\rho} + gh + \frac{v^2}{2} = Constant$$ And the pressure of air below the roof is high. When this pressure difference is excessive, the roof will lifted off due to net upward force and blows away.
6. Machine parts are jammed in cold days. Why?
The viscosity of a fluid increases with the decrease in temperature. With the increase in viscosity the internal fluid friction between two adjacent layers of fluid increases which opposes their relative motion. In cold days, the environmental temperature is less. As a result, the viscosity of the lubricating fluid in between the machine parts increase thereby decreasing the relative motion. So, the machine parts are jammed.
7. Airports at high elevation have longer runways for takeoffs and landings than do airports at sea level, why?
The plane takes a long run to achieve large velocity on the runways. The shape of the wings of the plane is so designed that the velocity of air above the wing is fast and below it is slow. According to Bernoulli's relation, $$E=\frac{P}{\rho} + gh + \frac{v^2}{2} = Constant,$$ the pressure above will be lesser than the pressure below. This pressure difference gives required upward force to lift the plane. The lift of a plane is possible if the upward force created on the wing due to difference in pressure above and below the wing is sufficient to overcome the gravitational pull on the plane.
The density of air is low compared to that at sea level, according to the above expression, the velocity should be increased to gain the required pressure difference to lift the plane. So, the airports have long runways at the high elevation than at sea level.
8. Small air bubbles rises slowly while big bubbles rise rapidly through the liquid. Why?
Air bubbles in the liquid experiences upthrust due to which it rises through the liquid. Upthrust is equal to the weight of liquid displace by the bubble, U = Vρg, where V is the volume of the bubble. Since, big bubbles has larger volume, more upthrust is experienced by it. Hence, the larger bubbles rises rapidly.
9. Define coefficient of viscosity and poise.
From Newton's formula for viscosity, $$F=-\eta A \frac{dV}{dx},$$
If A = 1, $$\frac{dV}{dx} = 1,$$ then $$\eta = - F$$
Hence, coefficient of viscosity of a fluid is defined as the viscous force acting per unit area of the layer having unit velocity gradient perpendicular to the direction of the flow of the fluid.
10. State Bernoulli’s theorem.
Bernoulli’s theorem states that for the stream line flow of an ideal liquid, the total energy per unit mass remains constant at every cross-section throughout the flow. $$ i.e., E=\frac{P}{\rho} + gh + \frac{v^2}{2} = constant$$
11. Define viscosity. Does it depend on temperature?
The property of a liquid by virtue of which it opposes the relative motion between its different layers is known as viscosity. Yes, the viscosity of the liquid depends on temperature, it increases with decrease in temperature.
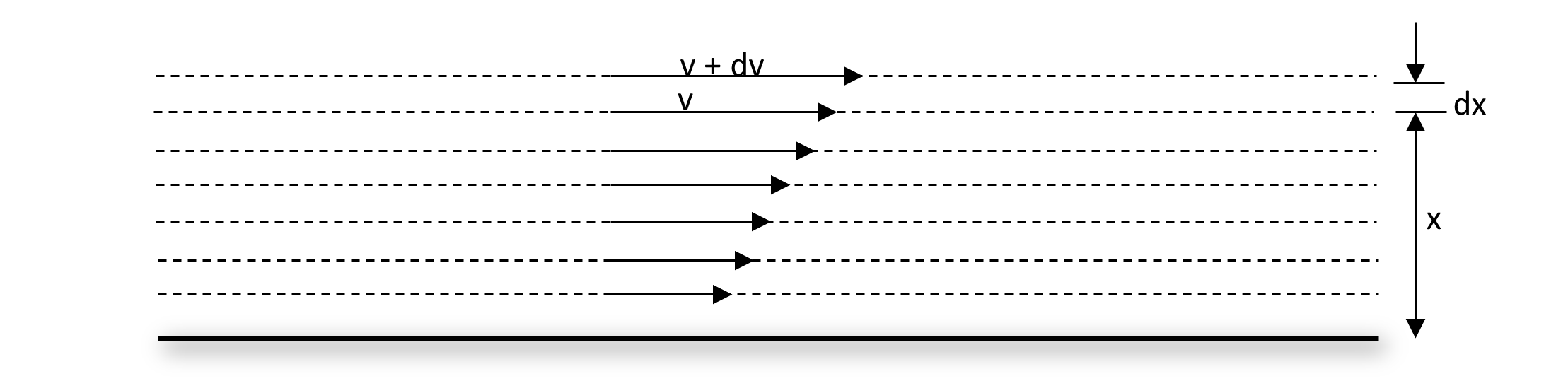
12. Explain with diagram, the meaning of velocity gradient in the case of liquid flowing in a tube.
Consider a fluid flowing steadily over a fixed surface as shown in figure. Each layer of fluid moving be parallel to the surface and have different velocity. The layer in contact with the surface will be at rest and the layers above will have velocities uniformly increasing upward. Thus there is variation in velocity with distance. This variation of velocity between layers separated by unit distance is called velocity gradient.
If the velocity of layer at distance x from the fixed surface be v and the velocity of the layer at distance x + dx be v + dv. Then, velocity gradient between the two layers is $$\frac{dV}{dx}$$